Národní shromáždění československé / Poslanecká sněmovna1920 – 1925

Generace budoucně do pojištěni přistupující.

Počet a stáří osob každoročně do pojištění přistupujících bylo by lze určiti dvěma metodami.

Jednak z počtu porodů jednotlivých roků, předcházejících zavedeni pojištění, z nichž při respektování pravděpodobnosti úmrtí této doby a čísel vystěhovalectví, jakož i přistěhovalectví, bylo by lze za předpokladu, že poměr počtu dělníků k veškerému obyvatelstvu se nezměnil, vypočísti srovnáním se skutečným stavem pojištěných osob, počet osob přistupujících v následujících po sobě letech do pojištění.

Použití této metody jest v daném případě znemožněno abnormálním průběhem počtu porodů a úmrtí v době válečné a poválečné, kromě toho silným přistěhovalectvím v prvních letech poválečných ze zemí bývalého Rakouska, jehož výši nelze zachytiti.

Bylo proto pro stanovení počtu osob přistupujících použito této druhé metody.

Předpokládáme-li, že zvětší se během jednoho roku počet osob pojištěním povinných stáří x v poměru udaném číslem c_x, jest počet osob přistupujících ve stáří x dán přibližně číslem

c_x M_x - M_X-1 (l^aa_x/l^aa_x-1),

při čemž zanedbáváme z důvodu bezpečnosti výpočtů a z nemožnosti přesného stanovení nepatrný počet osob v tomto roce vystupujících, pro něž neplatí převodní povinnost. [Čísel cit. pamětního spisu říšskoněmeckého z r. 1914, spisy říšského sněmu č. 144., 13. zákonodárná per. II. zasedání 1914/15, nelze vzhledem k převodní povinnosti podle §§ 239 - 243 této osnovy použíti.]

Podle uvedeného vzorce jsou vypočtená čísla přistupujících ročně mužů takto: N^m₁₅ = 55728, N^m₁₆ = 16013, N^m₁₇ = 12483, N^m₁₈ = 2092, N^m₁₉ = 274, a podobně pro ženy N^ž₁₅ = 30974, N^ž₁₆ = 12966, N^ž₁₇ = 6881 a N^ž₁₈ = 4431, celkem počet mužů každoročně do pojištění přistupujících 86.590 a žen 55.252. Při tom čísla l^aa_x jsou čísla žijících osob aktivních z řádu aktivnosti, odvozeného dále zvláště pro muže a zvláště pro ženy. Číslo c_x [Při volbě c = 1,01 byl by počet N^m_x v celém pětiletí vyšší o 3256 a osob N^ž_x o 1495, takže tato volba, již nelze pro celou budoucnost odůvodniti, neměla by vlivu na výši pojistného.] zvoleno při výpočtu čísel N^m_x, N^ž_x rovno 100 pro celé pětiletí x = 15 - 20.

Při výpočtu pojistného jest nutno dále počítati s tím, že vlivem přebytku porodů nad úmrtími přibývalo v posledních desetiletích neustále obyvatelstva, a tedy také obyvatelstva pojištěním povinného. Zanedbání této okolnosti vedlo by k přecenění zatížení. Bylo tudíž nutno počítati s přírůstkem čísel N^m_x a N^ž_x.

Srovnáním údajů o počtu dělníků a služebnictva podle výsledků sčítání lidu v roce 1900 a 1910 byly odvozeny tyto koeficienty přírůstku v desetiletých věkových skupinách pro dělníky a služebnictvo v Čechách, na Moravě a ve Slezsku, v periodě 1900 až 1910.

Ve stáří

Na základě těchto čísel byl by koeficient přírůstku pro jeden rok ve stáří 11 - 20 pro muže 1,016, tudíž procento přírůstku 1,6%, pro ženy 1,0243, tj. v procentech přírůstku 2,43% a pro obě pohlaví 1,0195, tedy 1,95%.

Pro následující výpočty byl zvolen koeficient přírůstku každoročních přístupů ve stáří 15 - 19, pro celý tento pětiletý interval c = 1,01 pro obě pohlaví.

Tato volba jest odůvodněna tím, že nelze v budoucnosti počítati s přírůstkem obyvatelstva tak intensivním jako v desetiletí 1900 až 1910, vzhledem k stálému klesání čísel porodů (která ani v letech 1921 a 1922 nedosahují čísel z r. 1911 [Viz dále tabulku č. 50.], které jen částečně může býti v celé budoucnosti vyváženo pak)!esem úmrtnosti.

Tabulka č. 50.

Mimo to nutno vzíti v úvahu, že čísla živě narozených dětí v letech 1915, 1916, 1917, 1918 i 1919 zůstávají vlivem válečných poměrů značně za čísly porodů dřívějších let a klesají v letech 1917 a 1918 pod jednu polovinu čísel dřívějších, jak je patrno z tabulky čís. 50.

Tento úbytek bude míti pravděpodobně za následek, že přístupy nových pojištěnců v letech 1930 až 1934 budou, nehledíme-li ku příznivějšímu snad průběhu úmrtnosti a vystěhovalectví, v témže poměru nižší jako jsou čísla porodů let 1915 - 1919 k číslům porodů let předcházejících.

Vliv této okolnosti projeví se přechodné také v hospodářství Ústřední sociální pojišťovny poklesem na příjmech z pojistného.

Aby však byl odhadnut vliv volby čísla c vyššího, byly provedeny také výpočty pro některé druhy nároků pro c = 1,014; výsledek těchto výpočtů pro nárok na invalidní a starobní důchod jest, že poskytují nepatrné snížení pojistného o 1,5%.

II. Početní podklady a výpočet základních čísel pro nároky na invalidní a starobní důchod.

Pro výpočet pojistného jest nejdůležitějším úkolem vhodná volba pravděpodobnosti invalidnosti a úmrtnosti aktivních pojištěnců, dále vhodná volba pravděpodobností výluky z požitku invalidního důchodu.

Tyto početní podklady slouží jednak k přímému výpočtu pojistných hodnot, jednak ke konstrukci řádu aktivnosti, který udává posloupnost čísel l^aa_x, tj. počet osob, které z původního počtu osob nejnižšího stáří jsou ve stáří x ještě na živu a aktivní. Volbě těchto početních podkladů byla proto věnována zvláštní pozornost a konstrukce řádu aktivnosti provedena novými metodami.

a) Pravděpodobnosti pro nastoupení invalidity. Pro volbu měrných čísel invalidnosti má pojistný matematik po ruce velmi sporý materiál, který nutil doposud k volbě čísel, o nichž bylo předem jisto, že nevystihují dobře průběh tohoto kolektivního zjevu, jehož vliv na finanční vývoj hlavního nositele pojištění je důležitý.

Tak byla zvolena pro výpočty předválečných předloh rakouských zákonů sociálního pojištění čísla, odvozená ze zkušeností na personálu německých drah nezúčastněném při vozbě, zpracovaných drem Zimmermannem; [Beiträge zur Theorie der Dienstunfähigkeits- und Sterbens- Statistik, 2. Heft, Berlin 1887.] avšak tato čísla již povahou materiálu, z něhož byla odvozena, který značným dílem zahrnuje také osoby v povolání jiném nežli dělnickém, dále úplně jiným pojmem invalidnosti, pak odlehlostí doby, v níž byla odvozena, konečně okolností, že vztahují se na osoby téměř výlučně pohlaví mužského, nehodí se za podklad výpočtů osnovy zákona o pojištění dělnickém.

To prokazovaly již dříve zkušenosti říšskoněmeckého invalidního a starobního pojištění zpracované až do roku 1894 a později za teta 1895 až 1897 v oficielních publikacích říšskoněmeckých [Denkschrift, betreffend die finanz. Entwicklung der Invaliditäts und Altersversicherungsanstalten u. der zugelassenen besonderen Kasseneinrichtungen, Berlin 1896. Pamětní spis č. 93. spisů říšského sněmu, 10. per. zákon. I. zas. 98/99.], které poskytují čísla o úplně jiném průběhu, při čemž čísla invalidnosti pozdějšího zpracování převyšují opět značně čísla zpracování dřívějšího.

Z tohoto sporého materiálu nebylo možno opatřiti si jiných podkladů a nebylo záhodno zvoliti čísla, nevystihující pravděpodobný průběh budoucí. Proto byla nastoupena tato cesta.

Přímo z materiálu uveřejněného v Amtliche Nachrichten des Reichsversicherungsamts ročníků 1908, 1909 a 1910 o počtu přiznaných důchodů u 31 ústavů invalidního a starobního pojištění (ústav 1. - 31.), dále z rozdělení podle věku pojištěnců, zjištěného říšskoněmeckým sčítáním podle povoláni v červnu r. 1907, a z počtu celoročních pojištěnců v letech 1906 až 1908, určeného pomocí počtu kvitančních známek odvedených v letech 1906, 1907 a 1908 u ústavů 1. - 31. [Zvoliti další nebo dřívější data než 1906 - 1908 nedoporučovalo se hlavně z toho důvodu, že z výkazů ústavů říšskoněmeckého invalidního pojištění nelze zjistiti počet a složení pojištěnců podle stáří; to může státi se pouze sčítáním, jež je prováděno ve 12letých periodách (1895, 1907) a hypotésami o přírůstku, jimiž spolehlivost odvození velmi trpí.], stanoveny střední koeficienty invalidnosti pro desetileté věkové skupiny, z nichž metodou Kingovou a formulí Karup-Spragueovou byly odvozeny koeficienty invalidnosti pro stáří 34 - 56. Tato čísla jsou v úplné shodě s čísly, uveřejněnými And. Lindstedtem pro účely národního pojištění švédského v oficielní publikaci Kostnadsberäkningar II. Alderdomsförsäkringskommittén, Stockholm 1912 a odvozenými způsobem blíže nepopsaným rovněž z říšskoněmeckých zkušeností invalidního a starobního pojištění z let 1906 - 1908 zvláště pro muže a pro ženy.

V tabulce č. 51. jsou ve sloupci 2. a 3. uvedena Lindstedtova čísla pro muže a ženy, v sloupci 5. vlastní naše čísla V_x odvozená přímo popsaným postupem z materiálu říšskoněmeckého pojištění a ve sloupci 4. průměrná čísla Lindstedtova pro obě pohlaví za předpokladu, že počet mužů je dvojnásobný počtu žen, jak odpovídá velmi přibližně složení kmene pojištěnců říšskoněmeckých v r. 1907 podle pohlaví (přesný poměr jest 663 : 337), tedy počítáno podle vzorce:

V_x = ¹/₃ (2 v^m_x + v^ž_x).

Tabulka č. 51.

Srovnání koeficientů invalidnosti.

Vzhledem k této shodě čísel V_x a V´_x zvolena pro následující výpočty čísla Lindstedtova odvozená ze zkušeností invalidního pojištění říšskoněmeckého v letech 1906 až 1908. Pro tuto volbu mluví okolnost, že jedná se o zkušenosti, odvozené z podobně definovaného okruhu osob pojištěním povinných, jak jej definuje osnova, dále o zkušenosti z materiálu velmi početného, neboť počet pojištěnců podle sčítání z 12. června 1907 obnášel u ústavů 1. - 31. 13,644.156 osob; dále okolnost, že definice invalidnosti říšskoněmeckého pojišťování kryje se s definicí invalidnosti podle tohoto zákona.

Kromě toho převyšují velmi značně pro rozhodující stáří čísla invalidnosti říšskoněmeckého pojištění příslušná čísla Zimmermannova, třebaže v číslech říšskoněmeckých není obsažena složka invalidnosti úrazové, pokud je kryta zvláštním pojištěním.

Mimo to berou čísla Lindstedtova ohled na úplně odlišný průběh invalidnosti u muži a u žen. Z tabulky právě uvedené (č. 51) jest patrno, že míra invalidnosti u žen převyšuje v letech 30 - 40 téměř dvojnásobně příslušná čísla pro muže, a teprve v ročnících stáří nad 60. rokem se těmto číslům poněkud blíží.

Z tohoto důvodu byly za účelem přesného odhadu zatížení u obou pohlaví výpočty provedeny zprvu zvláště pro každé pohlaví, a teprve ve výsledku sloučeny v jednotné pojistné (prémii).

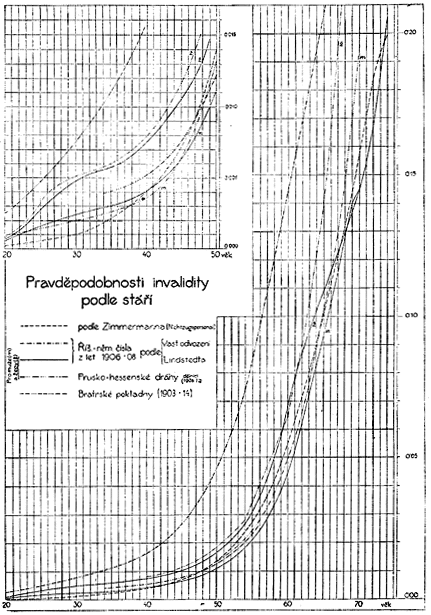
Ježto průběh čísel říšskoněmeckého invalidního pojištění v ročnících stáří nad 69 u mužů a v ročnících stáří nad 67 u žen, jak je patrno z grafického znázornění (viz diagram), zůstává pod čísly Zimmermannovými pro personál nesúčastněný při jízdě, byla čísla Lindstedtova doplněna po grafickém urovnání čísel pro x => 68 pro muže a x => 70 pro ženy, čísly Zimmermannovými. Diagram podává za účelem srovnání též průběh několika jiných, častěji používaných, nebo charakteristických tabulek pro pravděpodobnosti invalidity.

Takovýmto způsobem určeny roční pravděpodobnosti invalidnosti i_x udané v tabulkách III. a IV. příloh.

b) Pro konstrukci řádu aktivnosti a pro výpočet hodnoty důchodů invalidních jest dále nutno znáti pravděpodobnosti výluky z požitku invalidního důchodu.

V tomto směru použito bylo známé tabulky, odvozené ze zkušeností říšskoněmeckého pojištění o příjemcích důchodů přiznaných v letech 1891 až 1897, kteří požívali tohoto důchodu ještě v roce 1898, jakož i o příjemcích, kteří přibyli v letech 1898 a 1899, při čemž pozorování vztahovala se až do roku 1903.

Tyto velmi cenné zkušenosti, soustředěné v tabulkách výluky pro mužské a ženské důchodce, [Das Ausscheiden der Invalidenrentenempfänger der Jahre 1891 bis 1899 aus dem Rentengenuss. Amtliche Nachrichten des Reichsversicherungsamts, 1. Beiheft, Berlin 1906.] byly popsány často a dostatečně v odborné literatuře; jich podstatným znakem jest, že pravděpodobnosti výluky nezávisejí pouze na stáří, nýbrž též na trvání invalidity, pokud nepřevyšuje dobu 10 let.

Označíme-li s [m] + k pravděpodobnost výluky, že invalida, jenž vstoupil do stavu invalidity ve stáří a dožil se stáří m jako invalida, vystoupí z požitku invalidního důchodu před dosažením stáří m + k + 1, a označíme-li pⁱ (x, m) pravděpodobnost, že invalida, který stal se invalidou ve stáří jest ještě ve stáří x na živu a invalidou, jest

pⁱ (x, m) - (1 - s_[m]) (1 - s_[m]+1) (1 - s_[m]+2)... (1 - s_{[m]+x - m-1})

Při tom čísla s _{[m] + k} byla určena v uvedeném pramenu říšskoněmeckém pro k = 0 velmi důkladně z příslušných čísel pro jednotlivá čtvrtletí a tato opětně z pravděpodobností s pro jednotlivé měsíce; pro k = 1 až 4 určena rovněž z hrubého materiálu v jednotlivých čtvrtletích, a teprve pro k = 5 až 11 ze zkušeností jednotlivých roků. Ukázku těchto čísel s_{[m] + k} podává tabulka č. 52.

c) Pravděpodobnosti úmrtí osob aktivních q^aa_x nelze odvoditi přímo ze zkušeností invalidního a starobního pojištění, ježto, pokud neposkytují se nároky pro pozůstalé, nejsou případy úmrtí u aktivních pojištěnců z největší části hlášeny. Ale i tam, kde při úmrtí poskytují se nároky pro pozůstalé, zahrnují registrované případy úmrtí pouze část všech případů, totiž osob, které zanechávají oprávněné pozůstalé.

Tabulka č. 52.

Pravděpodobnost výluky z požitku invalidního důchodu po roce

Z toho a z jiných důvodů odvozují se tato čísla tím způsobem, že konstruuje se nejprve řád aktivnosti a z něho odvozují se čísla q^aa_x vztahem

l^aa_x+1 = l^aa_x (1 - q^aa_x - i_x)

d) Konstrukce řádu aktivnosti vzhledem k jeho mimořádné důležitosti pro všechny následující výpočty, byla provedena dvěma úplně odlišnými metodami, které poskytují téměř týž výsledek.

Jde o úkol velmi zajímavý po stránce vědecké a komplikovaný okolností, že čísla s_[m]+k respektive z nich odvozená čísla pⁱ (x, m), závisí na dvou argumentech.

K stanovení čísel l^aa_x jest nutno kromě čísel i_x a čísel pⁱ (x, m) znáti posloupnost čísel l_x, která udávají řád úmrtnosti celkového souhrnu osob aktivních i invalidů, na něž se pojištění vztahuje.

Úplně dostačující náhradou za tuto neznámou posloupnost čísel l_x jest řád úmrtnosti obyvatelstva vůbec, odvozený z čísel úmrtí v pětiletí 1906 - 1910 ze zkušeností na rakouském obyvatelstvu a z výsledků rakouského sčítání lidu k 31. prosinci 1910. [Oest. Statistik, Neue Folge, 1. Bd., 4. Heft.]

Tato čísla pečlivě zpracovaná a vyrovnaná Blaschkem novými metodami (metoda Brunsova pomocí Hermiteových polynomů) byla zvolena z toho důvodu, že vztahují se na velikou část obyvatelstva tohoto státu (kromě Slovenska), dále, že také dobou a metodou svého zpracování odpovídají požadavkům pro konstrukci čísel l^aa_x.

První použitá metoda vychází ze vztahu

l^aa_x = l_x - lⁱⁱ_x,

kde

lⁱⁱ_x = f^x_x0 l^aa (m) v (m) pⁱ (x, m) dm

a kdež v(x) je intensita invalidnosti ve stáří x a pⁱ (x, m) dříve popsaná pravděpodobnost, že invalida, jenž se stal v letech invalidním, dožije se jako invalida stáří x.

Tato rovnice integrální, jejíž jádro jest

K (x, m) = - v (m) pⁱ (x, m),

dovoluje určiti čísla l^aa_x řešením [Metoda jest popsána v pojednáních dra E. Schoenbauma: Příspěvek k matematické theorii invalidního pojištění. Časopis pro pěstování matem. a fys. roč. XLVII., str. 104 a násl.

Použití Volterrových integrálních rovnic v matematické statistice. Rozpravy č. Akademie 1917.], jež jest dáno rychle konvergující řadou

l^aa (x) = l (x) + E⁸₌₁ f^x l^aa (m) K⁽ⁱ⁾ (x, m) dm,

při čemž iterovaná jádra jsou

K⁽ⁱ⁾ (x, m) = f^x_m K (x, z) K⁽ⁱ⁺¹⁾ (z, m) dm.

Jestliže klademe

l^aa (x) = l (x) + E⁸_k=1 f_k (x),

můžeme dokázati na základě věty Dirichletovy, že jest

f_k (x) = f^x_x0 K (x, z) f_k-1^(z) dz

a označíme-li

f_k(x) = - v (x) f_k-1 (x)

f₁ (x) = v (x) l (x),

bude

f_k (x) = f^x_x0 f_k^(z) pⁱ (x, z) dz

Tabulka č. 53.

Numerický výpočet hodnot l^aa (x) pomocí řady čísel f_k (x) použitím známých součtových metod děje se pomocí obratů, jejichž uveřejnění jest vyhraženo zvláštnímu spisu, velmi jednoduše a rychle, neboť zvláště pro x menší 50 konverguje řada f_k (x) tak rychle, že stačí k výpočtu použíti kromě f₀ (x) = l (x) ještě f₁ (x), f₂ (x) a f₃ (x). Skutečně jest f₃ (x) až do x = 45 menší než 0,5.

Tato konvergence jest patrna z tabulky čís. 53. Pro x menší 50 jest ovšem konvergence volnější.

Druhá metoda použitá v této formě rovněž po prvé vychází také ze vztahu

l^aa_(x) = l_(x) - f^x_x0 l^aa (m) v (m) p¹ (x, m) dm

Spočívá však v tom, že integrál na pravé straně rozdělí se na tři části, z nichž prvá obsahuje půl intervalu počátečního a třetí půl intervalu koncového. Prostřední pak součet integrálů, jichž hranice liší se o jedničku.

Je tedy

l^aa (x) = l (x) - f^x0+1/2_xo l^aa (m) v (m) pⁱ (x, m) dm - E^x-1_t=x0+1 f^t+1/2_t-1/2 l^aa (m) v (m) pⁱ (x, m) dm +

- f^x_x-1/2 l^aa (m) v (m) pi (x, m) dm = l (x) - A (x) + B (x) + C (x)

Výhoda tohoto rozložení oproti obvyklému postupu záleží v tom, že použitím věty o střední hodnotě lze funkci B (x) počítati přímo z tabulkových hodnot s_(x)+k. Užijeme-li pak vztahu

f^t+1_t i^aa (z) v (z) dz = l^aa (t) i (t).

kde i (t) jest roční pravděpodobnost invalidisace, dostaneme:

A (x) = f^x0+1/2_x0 l^aa (m) v (m) pⁱ (x, m) dm

B (x) = E^x-1_t=x0+1 f^1+1/2_t-1/2 l^aa (m) v (m) pⁱ (x, m) dm = E^x-1_t=x0+1 pⁱ (x, t + g) l^aa (t - ¹/₂) i (t - ¹/₂),

C (x) = f^x_x-1/2 l^aa (m) v (m) pⁱ (x, m) dm = pⁱ (x, x - g) a laa (x - 1) i (x -1),

kdež jest

0 < g < ¹/₂, 0 < a < 1

- ¹/₂ < g < ¹/₂,

0 < g < ¹/₂, 0 < a < 1

Položíme pak

g = 0, a = ¹/₂,

g = 0

g = ¹/₄, a = ¹/₂,

x₀ = 20

Čísla pⁱ (x, x - ¹/₄) vypočítáme kvadratickou interpolací z hodnot

pⁱ (x, x - 1) = 1 - s_[x-i]

pⁱ (x, x - 2) = [1 - s_[x-2]] [l - s_[x-2]+1]

pⁱ (x, x -¹/₄) = ²¹/₃₂ + ⁷/₁₆ pⁱ (x, x - 1) ³/₃₂ pⁱ(x, x - 2)

při čemž s_{[x] + k} jest pravděpodobnost (selekční), že invalida, jenž vstoupil do stavu invalidity jako xletý a dožil se stáří x + k, zemře během roku x + k až x + k + 1.

Při provádění výpočtů vede k značnému zjednodušení omezení selekce na 10 a méně než 10 roků.

Podrobnosti výpočtů provedených zvláště pro muže a pro ženy jsou patrny z tabulek I. až IV. uvedených v příloze.

Z těchto tabulek budiž zde uveden výtah (tab. č. 54) (pro muže).

Obě metody vedou, jak patrno z tabulky č. 55, k výsledkům téměř úplně shodným, uvážíme-li zvláště, že postupují nestejnými obraty k docílení numerických výsledků.

Za podklad dalších výpočtů zvolen řád aktivnosti vypočítaný metodou druhou.

Scházející čísla l^aa(x) pro x < 20 byla doplněna podle vzorce

l^aa_x = l^aa_x-1/1 - q^aa_x - i_x

kdež q^aa_x vzato rovno q_x, tj. pravděpodobnosti úmrtí z obecné tabulky úmrtnosti rakouského obyvatelstva z r. 1906 - 1910.

Výsledek tohoto prodloužení jest obsažen v připojených tabulkách.

Tabulka č. 54.

Tabulka č. 55.